Das Fluss- und Ultrafiltrationssystem hat sowohl einen definierten Dialysatfluss antiparallel zum Blutstrom durch den Dialysator als auch einen definierten Konvektionsfluss (<< Dialysatfluss) durch die Dialysatormembran zu realisieren. Im vorliegenden Fall wird der Konvektionsfluss durch Aufbau einer möglichst konstanten steuerbaren Druckdifferenz über der Dialysatormembran erzeugt, indem der Dialysatdruck dem vom Bluttransportsystem erzeugten Druck innerhalb der Hohlfasermembran nachgeführt wird. Technisch realisiert werden die beiden Aufgaben durch zwei hydraulisch in Reihe vor und nach den Dialysator geschaltete Zahnradpumpen, wobei in Abhängigkeit der Drehzahlverläufe beider Pumpen sowohl ein bestimmter Fluss durch Pumpen und Dialysator durch als auch ein bestimmter Druck zwischen beiden Pumpen aufgebaut wird, der den Konvektionsfluss bestimmt.

Die zwei Steuer- bzw. Regelungsysteme müssen folgenden Anforderungen genügen:
1. Die Präzisionsanforderungen an den Fluss sind relativ unkritisch; er muss so groß sein, dass im Dialysator stationäre Konzentrationsprofile der ausgetauschten Stoffe aufrecht erhalten werden; es geht in erster Linie darum, den Fluss konstant zu halten und Störungen besonders in Richtung niedriger Flüsse, schnell abzubauen
2. Weitaus kritischer sind die Anforderungen an das System, das den Konvektionsfluss resp. den Dialysatdruck steuert: Die Anforderungen an die Dynamik des Konvektionsflusses sind zwar funktionell ähnlich unkritisch wie an die des Dialysatflusses, die Patientensicherheit fordert aber, um die Infektion des extrakorporal geführten Blutes bei zeitweiser, partieller Bewässerung auszuschließen, grundsätzlich einen Konvektionsfluss in Richtung Dialysat und damit eine minimale Druckdifferenz zwischen Blut- und Dialysatkreis. Die Dialysatdruckregelung ist also als Folgeregelung mit dynamischen Anforderungen, die sich durch den Druckverlauf auf der Blutseite ergeben, zu realisieren.
Da der Druckverlauf auf der Blutseite insbesondere bei diskontinuierlichem, periodischem Bluttransport (Single Needle) bereits durch die Maschine realisiert wird (steilster Anstieg bzw. Abfall des Drucks auf der Blutseite beim Öffnen des venösen Klemmventils), können kritische Zustände vorab erkannt und in den Reglerentwurf einbezogen werden.

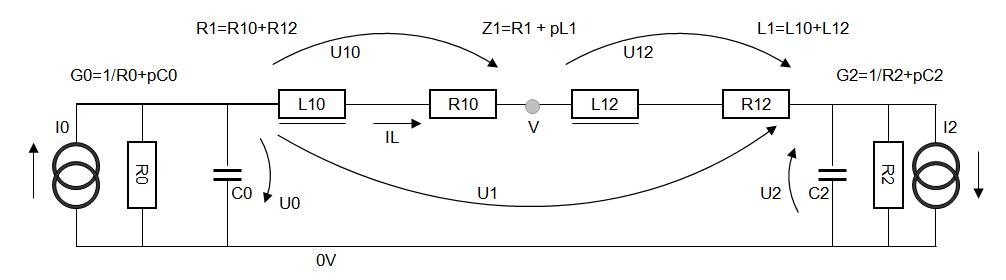
Das Hydrauliksystem zwischen Entnahmestelle (Heizergefäß) und Ablauf wird als Kette von hydraulischen Widerständen und zwei Antrieben angesehen, für den Strom insbesondere zwischen den Pumpen wird Kontinuität vorausgesetzt, s.o. Sieht man die Zusammenhänge zwischen dem durch die Pumpen aufgebauten Druck und dem sich einstellenden Fluss grob vereinfacht als linear an, so lässt sich das Hydrauliksystem in Analogie zur Elekrotechnik durch folgende Maschen- und Knotengleichungen beschreiben, s.o.:

(1) U1=U0+U2 mit U1=ZL*IL, Maschengleichung
(2) I0=IL+G0*U0, Knotengleichung Pumpe 0
(3) I2=IL+G2*U2, Knotengleichung Pumpe 2
mit dem mittleren Dialysatdruck V:
(4) V=(1-a)*U0-a*U2, a kann komplex sein.
Die Eigenwerte von IL des oben angegeben Gleichungssysstems unterscheiden sich von denen der von den Pumpen aufgebauten Drücke U0,U2 um mindestens eine Größenordnung; die Werte sollten dementsprechend mit verschiedenen Taktraten abgetastet und verarbeitet werden. (1..3 bzw. 4) ergibt bereits ein MIMO-System 3.Ordnung, unter Einbeziehung der Modelle für die DC-Antriebe ein unvorteilhaft zu handelndes MIMO-System 7.Ordnung als Streckenmodell.

Geht man davon aus, dass die komplexen Leitwerte G0 und G2 gleiche Phasenwinkel (G0=c*G2, c reell) und folglich die Systeme U0 und U2 gleiche Zeitkonstanten besitzen, vereinfacht sich die Abhängigkeit des Potenzials für bestimmtes, nunmehr reelles a von der Differenz der Pumpenflüsse (I0-I2) zum pT1-Verhalten mit der gleichen Zeitkonstanten:

(5) V(a)/(I0-I2) = c/(1+c) * 1/G0 bei a=G2/(G0+G2)

Für konstante Flüsse, damit U1=const., folgt darüber hinaus nicht nur für V(a), sondern für alle Potenziale V, also an beliebigen Stellen zwischen U0 und U2 das gleiche Verhalten (4):

(6) V= (1-a)U0-a(U1-U0)=U0-aU1, U1=const.

Der Potentialverlauf von U0 nach U2 wird also bei gleicher Steigung U1 durch unterschiedliche (I0-I2) nur vertikal mit pT1-Verhalten um die Änderung von U0 verschoben.

Für die den Dialysatfluss bestimmende Summe der Drücke U1=U0+U2 ergibt sich eine ähnliche Abhängigkeit von der gewichteten Summe der Pumpenflüsse (I0+c*I2):

(7) U1/(I0+c*I2)=1/(G0 + (c+1)/R1),
für Zeitintervalle mit näherungsweise konstanten Dialysatfluss (pLL << R1)

Damit könnte das MIMO-System zu zwei Systemen für Druck und Dialysatfluss entkoppelt werden. I.a. ist die o.g. Voraussetzung G0=c*G2, c reell, allerdings nicht gegeben. Sind U0 und U2 aber messbar, und lässt sich beiden Drücke ein gewünschtes, identisches Zeitverhalten aufprägen und damit lassen sich die eben angestellten Überlegungen anwenden.

Dies wird durch spezifisch dimensionierte Regler für beide Pumpen erreicht. Für einen ersten Entwurf ist ein Zustandsregler mit Polverschiebung, mit denen man eine vorgegebene Dynamik sehr einfach realisieren kann, sinnvoll (2x SISO-System 3. Ordnung). Praktisch, vor allem angesichts der zu berücksichtigenden Nichtlinearitäten und Unsymmetrien in der Implementierung besser zu handhaben ist eine dynamisch vergleichbare Kaskadenregelung (Pumpenstrom, -drehzahl, Druck).

Wie bereits erwähnt, sind aufgrund unterschiedlicher Eigenwerte resp. Zeitkonstanten für den Druckaufbau auf der einen und für Dialysatfluss (und Konvektionsstrom) auf der anderen Regler mit unterschiedlichen Zeitkonstanten angebracht. Im schnellen Kreis wird entsprechend (2),(3) und den zugehörigen DC-Antriebsmodellen der Druckaufbau U0 bzw. U2 entkoppelt geregelt, mit dem Ziel, identische Zeitkonstanten und damit die Gültigkeit von (5) zu erreichen (s.o.). Die Sollwerte für die Drücke U0,U2 werden allerdings durch den Zustandsregler bei den unvermeidlichen Modellungenauigkeiten bzw. -fluktuationen nur näherungsweise erreicht.

Die Sollwerte für die benötigten Drücke U0,U2 liefert der äußere Regelkreis, also die Regler für Konvektionsstrom (Ultrafiltrationsrate bzw. -volumen, Input Transmembrandruck, Differenz zwischen V und dem Druck des extrakorporalgeführten Blutes) und Dialysatfluss (Input: gewichtete Summe der Drücke U0,U2). Diese äußeren Regler sind jeweils SISO-Systeme 2. Ordnung. Durch das integrierende Verhalten der äußeren Systeme wird das Erreichen des Sollwertes im stationären Fall mit der nötigen Genauigkeit realisiert.